[MATH] Really complicated stuff.

[insignia96]

Okay,

First off, i am a math n00b. I dont have a degree in math and dont know any math beyond pre-algebra. I am an advanced math student, but i dont understand what i need to do. I have googled it and read alot of stuff, but i need someone to help me with this.

I am making a 3D model of the solar system in AutoIt with a 3D plugin. I need an elliptical orbit around the sun for most (all) of the planets. I need a function to calculate the elliptical orbits. I know tha at the minimum Earth is 0.98 AU from the sun and at maximum it is 1.02 AU away. Is there any way to accomplish an equation(s) that i can put those two values and have the result be the radius for a circular orbit so it appears elliptical.

Please tell me if you need more info to help me.

[nothinglol]

i don't feel like writing math.

so i'll direct you to something that may (or may not) be what you are looking for

Elliptical Orbits

EDIT: think I found it, check below

[andykh]

Never say your real age on the interwebz.

inb4pedobear

[nothinglol]

got it now I beleive!

in, for example, this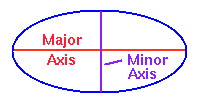

You already have the measurements, and so you should apply the major axis variable A (1.02 AU) and the minor axis variable B (.98 AU)

you can then calculate the eccintricity (how much it flattens) using the equation:

b^2=a^2(1-e^2)

EDIT: forgot to mention, I won't do the math for you

EDIT EDIT: That is assuming that the sun is exactly centered. I think for what you are doing that is alright, but if you're that bright young student shouldn't you shoot for astronomically correct?

Give me one minute and I'll add some MORE math hehe

EDIT EDIT EDIT: well would you look at that, this site *should* also tell you some stuff to check out

http://spiff.rit.edu/classes/phys440...e/ellipse.html

[insignia96]

Will study this later and post back. This looks right though.

[magnajohn622]

This is more of a physics question than a math question. Get a pencil and paper out because you probably will need to visualize most of this stuff.

Basically, an ellipse has 2 focal points, both on the major axis of the ellipse (the longer axis). Looking at the sun/planet relationship, the sun is one of these focal points. There is no physical second focal point. Now, if you take any point on an ellipse and measure the distance from each focal point (call them r1 and r2), r1 + r2 is constant (call it K). K is also equal to the major axis, which is also the sum of the closest distance to one focal point plus the furthest distance from that same focal point. In this case, K=2. One of the other rules of an ellipse is that the 2 focal points are equidistant from the center of the ellipse. To find the location of the focal points is simple.

If r1 is the distance from a point on the ellipse to the sun, and r2 is to the other focal point, then:

K=r1+r2
2=r1+r2

At the closest point to the sun:

2=.98+r2
r2=1.02

So since the major axis = 2, the center of that axis = 1, and we can say that each foci is .02 AU away from the center.

So now we know where each focus is.

Now we need an equation for the x,y coordinates of all the points on an ellipse.

Let f be the distance from the center to either focal point. Let r1 be the distance from one focal point to a point on the ellipse x,y. Let r2 be the distance from the other focal point. Using some trigonometry, we can say that:

(x+f)^2 + y^2 = r1^2
sqrt((x+f)^2 + y^2) = r1
and
(x-f)^2 + y^2 = r2^2
sqrt((x-f)^2 + y^2) = r2

We know that r1 + r2 = the major axis, a, so:

sqrt((x+f)^2 + y^2) + sqrt((x-f)^2 + y^2) = 2a

Now simplify to get rid of one of the sqrt functions, and we get (i'm skipping a lot of steps here, so you probably want to work this out for yourself):

sqrt((x-f)^2 + y^2) = a - (f/a)x

Now square both sides to simplify, and it comes out to be (again, i'm skipping a lot of steps):

1 = (x^2/a^2) + (y^2/((a^2)-(f^2)))

and

x = a*sqrt(1 - (y^2/((a^2)-(f^2))))
and
y = sqrt((1 - (x^2/a^2))*(a^2 - f^2))

The above are the functions that you need to use.

And that's it. It looks a lot cleaner on paper. I'm not a programmer though, so i wouldn't know how to write a program to draw one for you but that's the function. I'm pretty sure that's all correct, but if anyone catches an error let me know.

EDIT: I just remembered something, i think this can be simplified further. There's a way to simplify it to show that a^2 - f^2 = b , where b is the minor axis I don't remember how to show this but you can substitute that into the equation.

[insignia96]

I think when i am less tired teh maths i have got now should be able to calculate what i need to know.

[Hellgawd]

Failure, indeed.

[ReidE96]

Here I thought I could forget all that stuff from FP3. Oh well. If you still need help, I'll dig out the formulae I memorised long enough for the exam and start throwing stuff at you.