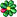a = 1 (filler)
Shout-Out
User Tag List
Results 1 to 15 of 72
-
03-09-2009 #1Contributor


- Reputation
- 121
- Join Date
- Feb 2007
- Posts
- 193
- Thanks G/R
- 0/0
- Trade Feedback
- 0 (0%)
- Mentioned
- 0 Post(s)
- Tagged
- 0 Thread(s)
Calculate this and get a FullInfoAccount
Last edited by blubb12345; 03-12-2009 at 03:08 PM.
$50 SUBWAY CARD GIVEAWAY >> https://bit.ly/aMbaU5 << LIMITED TIME OFFER
-
03-09-2009 #2Active Member


- Reputation
- 49
- Join Date
- Oct 2007
- Posts
- 232
- Thanks G/R
- 0/0
- Trade Feedback
- 0 (0%)
- Mentioned
- 0 Post(s)
- Tagged
- 0 Thread(s)
-
03-09-2009 #3Contributor


- Reputation
- 121
- Join Date
- Feb 2007
- Posts
- 193
- Thanks G/R
- 0/0
- Trade Feedback
- 0 (0%)
- Mentioned
- 0 Post(s)
- Tagged
- 0 Thread(s)
-
03-09-2009 #4Banned

- Reputation
- 6
- Join Date
- Feb 2009
- Posts
- 98
- Thanks G/R
- 0/0
- Trade Feedback
- 1 (100%)
- Mentioned
- 0 Post(s)
- Tagged
- 0 Thread(s)
a=0.69314718055994530941723212145818
passes through (0.5,0)
Not sure what you mean to be honest.
-
03-09-2009 #5Active Member


- Reputation
- 32
- Join Date
- Nov 2008
- Posts
- 130
- Thanks G/R
- 0/0
- Trade Feedback
- 0 (0%)
- Mentioned
- 0 Post(s)
- Tagged
- 0 Thread(s)
x=1
whoohoo!!!"If Man realizes technology is within reach, he achieves it. Like it's damn near instinctive."
--Ghost in the Shell
-
03-09-2009 #6Contributor


- Reputation
- 121
- Join Date
- Feb 2007
- Posts
- 193
- Thanks G/R
- 0/0
- Trade Feedback
- 0 (0%)
- Mentioned
- 0 Post(s)
- Tagged
- 0 Thread(s)
2. wrong
3. wrong
$50 SUBWAY CARD GIVEAWAY >> https://bit.ly/aMbaU5 << LIMITED TIME OFFER
-
03-09-2009 #7Banned

- Reputation
- 6
- Join Date
- Feb 2009
- Posts
- 98
- Thanks G/R
- 0/0
- Trade Feedback
- 1 (100%)
- Mentioned
- 0 Post(s)
- Tagged
- 0 Thread(s)
Wait, I'm stupid.
a=0.34657359027997265470861606072909
passes through (1/sqrt(2),0)
-
03-09-2009 #8Active Member


- Reputation
- 55
- Join Date
- Jan 2007
- Posts
- 504
- Thanks G/R
- 0/0
- Trade Feedback
- 0 (0%)
- Mentioned
- 0 Post(s)
- Tagged
- 0 Thread(s)
lol it is f(x)=1/x

 NoT A ZomBie~BuT iLL~EaTuRBrainS
NoT A ZomBie~BuT iLL~EaTuRBrainS
-
03-09-2009 #9Banned

- Reputation
- 145
- Join Date
- Jan 2009
- Posts
- 745
- Thanks G/R
- 0/0
- Trade Feedback
- 0 (0%)
- Mentioned
- 0 Post(s)
- Tagged
- 0 Thread(s)
a= (1 . 1)
EDIT: I mean X coordinate 1,y coordinate 1Last edited by wow4Supplier; 03-09-2009 at 12:18 PM.
-
03-09-2009 #10Contributor


- Reputation
- 121
- Join Date
- Feb 2007
- Posts
- 193
- Thanks G/R
- 0/0
- Trade Feedback
- 0 (0%)
- Mentioned
- 0 Post(s)
- Tagged
- 0 Thread(s)
still no right answer
$50 SUBWAY CARD GIVEAWAY >> https://bit.ly/aMbaU5 << LIMITED TIME OFFER
-
03-09-2009 #11Contributor


- Reputation
- 161
- Join Date
- Oct 2006
- Posts
- 487
- Thanks G/R
- 15/6
- Trade Feedback
- 3 (100%)
- Mentioned
- 1 Post(s)
- Tagged
- 0 Thread(s)
My girlfriend's guess is 0 :P
-
03-09-2009 #12Active Member


- Reputation
- 55
- Join Date
- Jan 2009
- Posts
- 298
- Thanks G/R
- 0/0
- Trade Feedback
- 0 (0%)
- Mentioned
- 0 Post(s)
- Tagged
- 0 Thread(s)
Wuergh i'm stupid at Maths but I love peter Fox and I'm german too gief
 !
!
No srsly it's something like 0,3 ...
PM me for Signatures!
-
03-09-2009 #13Banned

- Reputation
- 95
- Join Date
- Oct 2007
- Posts
- 654
- Thanks G/R
- 0/0
- Trade Feedback
- 0 (0%)
- Mentioned
- 0 Post(s)
- Tagged
- 0 Thread(s)
Aww.. must think about it
 I will edit my post later and tell ya
I will edit my post later and tell ya
-
03-09-2009 #14Archer



- Reputation
- 470
- Join Date
- Dec 2006
- Posts
- 1,625
- Thanks G/R
- 1/1
- Trade Feedback
- 0 (0%)
- Mentioned
- 0 Post(s)
- Tagged
- 0 Thread(s)
Find a value of a such that the area beneath the curve is 0.5
Area beneath f(x) is integral of f(x)
Integral of f(x) = integral of ln(x) + ax +c
=xlnx + ax + c - integral of 1
=xlnx +(a-1)x + c
Upper limit is 1 always, lower limit is... hmmm....
1ln(1) + a - 1 - (xlnx + (a-1)x) = 0.5
a - xlnx - ax + x = 1.5
a(1-x) = 1.5 + x(lnx - 1) = (1.5 + x(lnx-1))/(1-x)
Find the lower limit of x, plug it in, get your answer!
Edit: Thought a little more.
Lower limit is where f(x) = 0 so
ln(x) = -a
x = 1/(e^a)
1ln(1) + a - 1 - (-a/(e^a) + (a-1)/(e^a)) = 0.5
a + a/(e^a) - (a-1)/(e^a) = 1.5
a + e^-a = 1.5
a + 1/(e^a) = 1.5
ae^a + 1 = 1.5e^a
(a - 1.5)e^a = -1
Yeah, I cba now, dinner's ready Enjoy folks!
Enjoy folks!
Edit again: Back from dinner, and seeing as noone has it yet I'll push on.
a + e^-a = 1.5
e^-a = 1.5 - a
We know ln(x) + a = 0 at x = e^(-a)
But we also know e^(-a) = 1.5 - a
So ln(1.5 - a) + a = 0
ln(1.5)/ln(a) = -a
ln(1.5) = -aln(a)
ln(1.5) = ln(a^-a)
a^-a = 1.5
a^a = 2/3
Ok, that's just great.
Lemme try again, from (a - 1.5)e^a = -1
ln of both sides: ln((a-1.5)e^a) = -1
ln(a-1.5) + ln(e^a) = -1
ln(a-1.5) = -a - 1
a = 1.5 + e^(-a - 1)
a = 1.5 + (e^-a)/(e^-1)
a = 1.5 + (e^1)/(e^a)
a = 1.5 + e*e^(-a)
But e^-a = 1.5 - a, so
a = 1.5 + e(1.5 - a)
a = 1.5(1+e) - ea
a(1+e) = 1.5(1+e)
a = 1.5
WOO! Now, common sense tells me something's wrong there. But I don't care
Last edited by ReidE96; 03-09-2009 at 01:41 PM.

-
03-09-2009 #15Banned

- Reputation
- 6
- Join Date
- Feb 2009
- Posts
- 98
- Thanks G/R
- 0/0
- Trade Feedback
- 1 (100%)
- Mentioned
- 0 Post(s)
- Tagged
- 0 Thread(s)
You have to solve
1.5=exp(-a)+a
Similar Threads
-
Come to this Website and get your youtube gaming videos watched quickly! :)
By JesseBascom in forum Community ChatReplies: 2Last Post: 05-26-2016, 02:38 PM -
Will this video card run max settings and get 20 fps or more
By Liquid Malfunction in forum World of Warcraft GeneralReplies: 4Last Post: 02-16-2009, 05:22 PM -
Edit Druid Forms - Please, every druid want this, do this and you will get big credit
By Hylde in forum WoW ME Questions and RequestsReplies: 10Last Post: 01-05-2007, 07:52 PM -
Levle 51+ and get rep&honer
By vandethgo in forum World of Warcraft GuidesReplies: 2Last Post: 12-18-2006, 12:29 PM -
Put fake auction up and get a shard from it
By Destar in forum World of Warcraft ExploitsReplies: 17Last Post: 12-05-2006, 09:44 PM